Transportation_TRA_LP1. Перевозка товаров, транспортная задача, Монж-Канторович. Минимум затрат на перевозку товаров от производств потребителям. Планирование поставок, логистика, ритейл. 1 интервал.

Постановка задачи

Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки. Транспортная задача по теории сложности вычислений входит в класс сложности P. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).

Дано:

•  Производители товара, каждый производит определенного количество товара.

•  Потребители товара, каждый имеет собственную потребность в товаре.

Требуется:

Найти распределение товаров производителей по потребителям, составляющее минимум затрат на транспортировку.

кратко

Число установок соответствует числу производителей товаров.

Установка отражает распределение произведенного товара одного производителя по потребителям.

Операциями установки является доставка некоторого объема товара потребителю.

Потоками операции являются объем товара, который доставляется потребителю: уменьшение запаса производителя, удовлетворение потребности потребителя.

Условия:

Для потоков операций установок задается ограничение баланса – насколько уменьшился запас производителя, настолько и удовлетворилась потребность потребителя (объем доставки).

Для задания потребности потребителей используются ограничения на границы емкости в конце горизонта.

Для задания объемов производства используются остатки емкостей в начале горизонта и границы емкостей в конце горизонта.

Критерий – минимум суммарной стоимости доставки товаров. Для минимизации стоимости доставки используется критерий «прибыли/издержек от выполнения операций». Стоимость выполнения операции равна расстоянию от производителя до потребителя, деленному на 2 (поток дублируется – один входящий, другой выходящий).

кратко

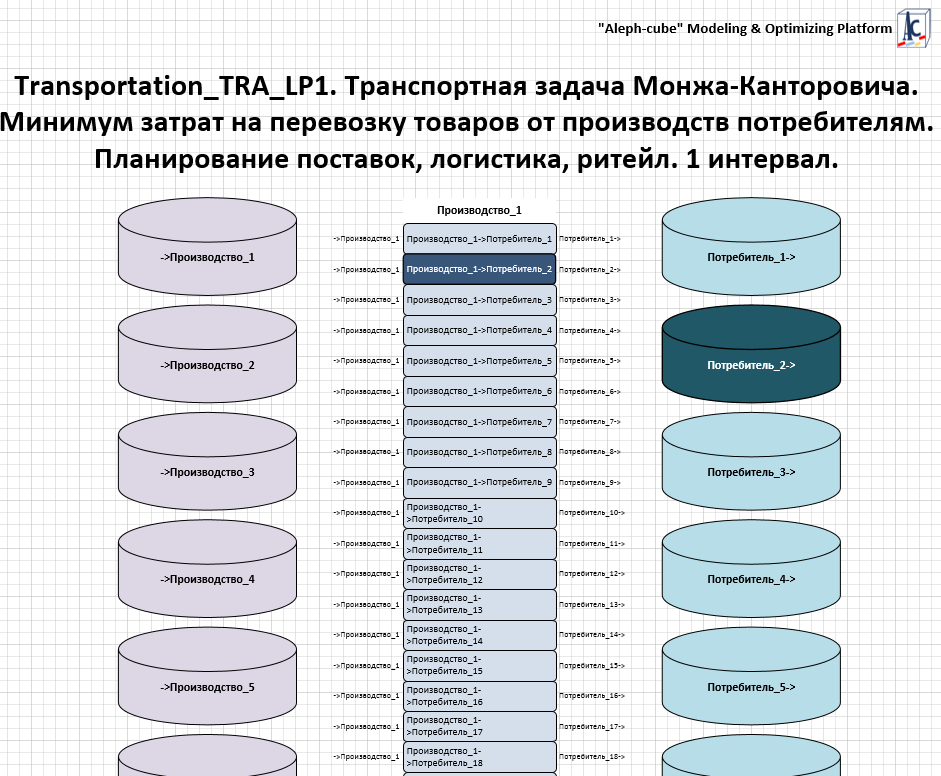
Рисунок. фрагмент потоковой схемы объекта «с именами»

кратко

Цены доставки товаров от производств к потребителям

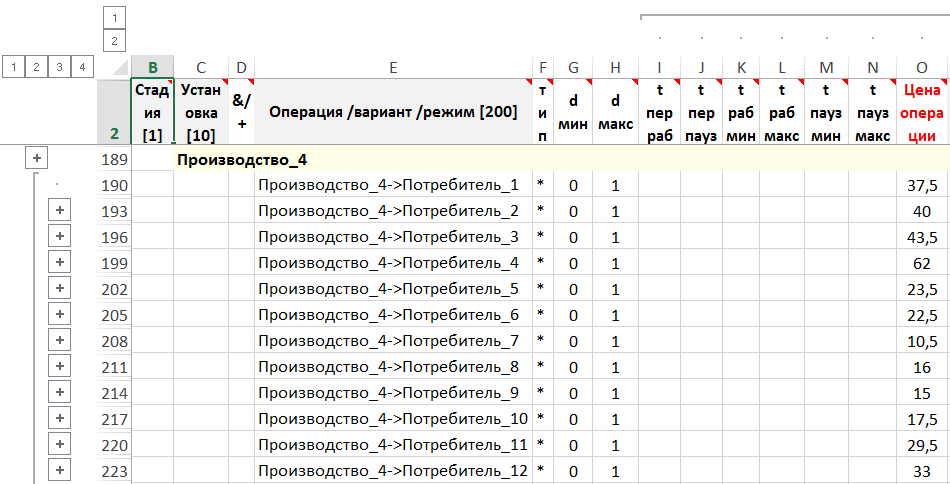
Рисунок. Фрагмент формы – стадия, установка, операция, поток

Критерий задачи – минимум стоимости выполнения операций, что соответствует минимальной стоимости доставки товаров.

кратко

Выбор доставки товара от производства

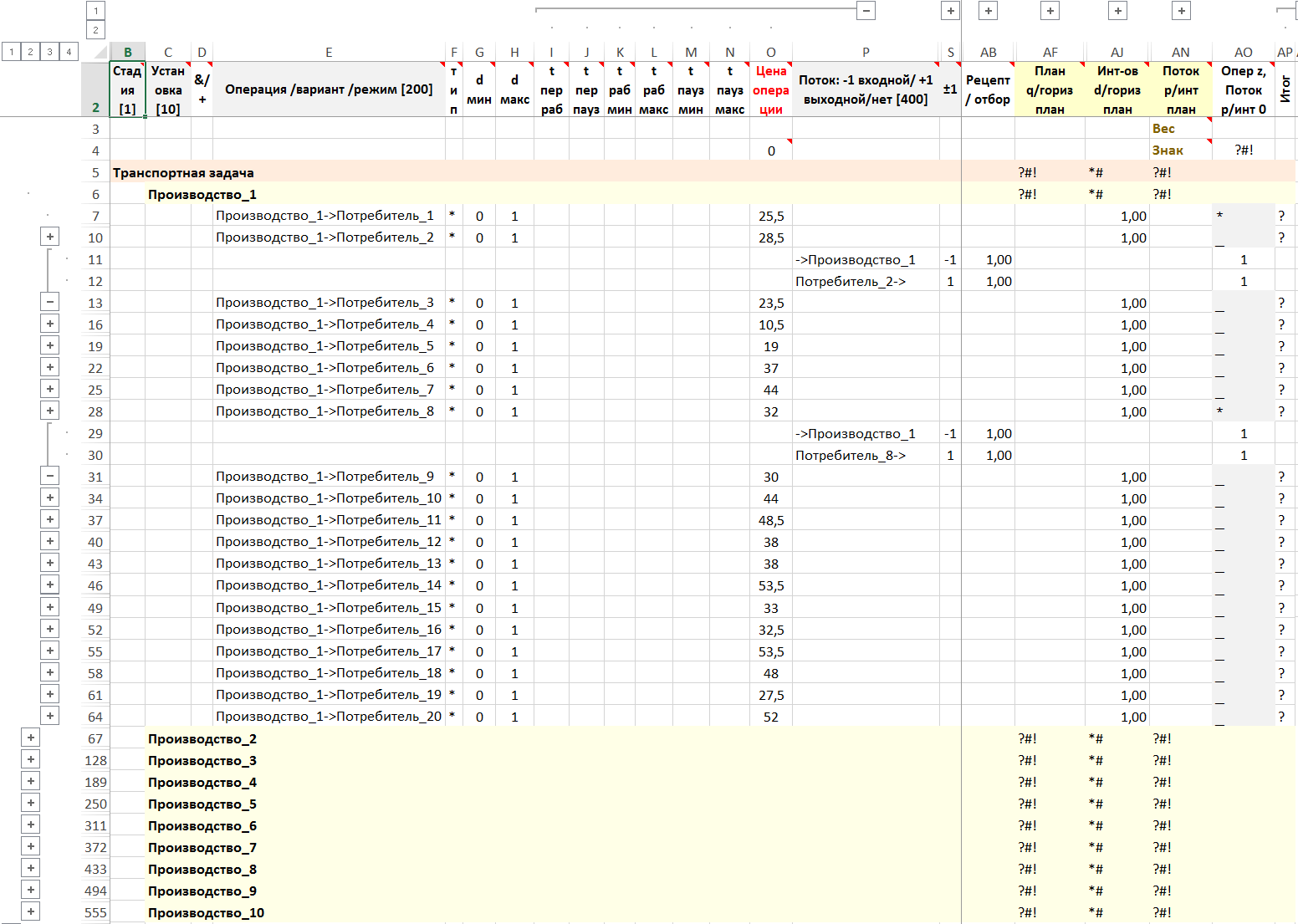
Рисунок. Фрагмент формы – стадия, установка, операция, поток

Запасы товара в производствах для доставки.

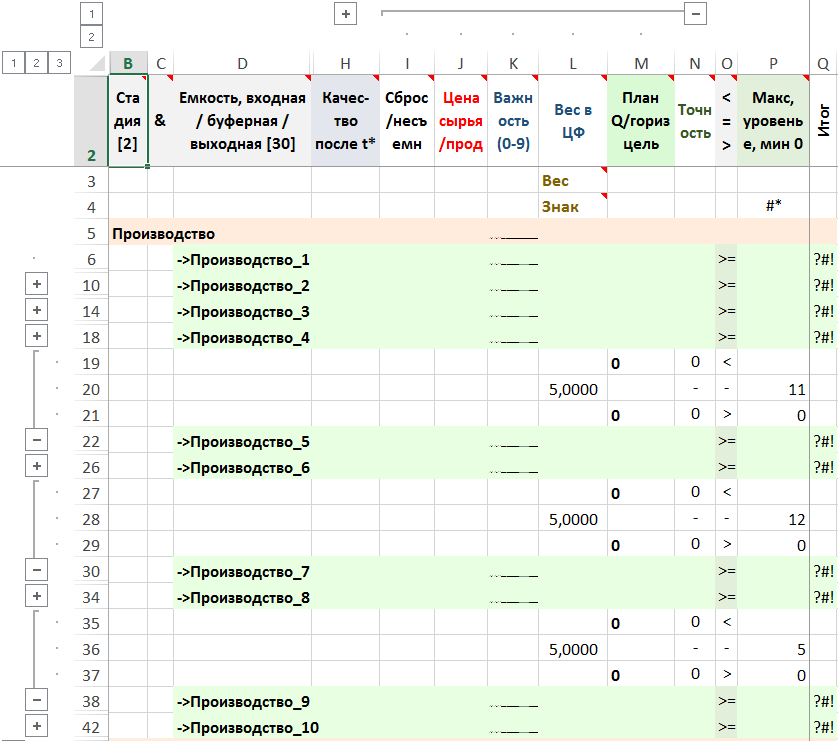
Рисунок. Фрагменты формы – стадия, емкость

Примечание. Запасы товаров по мере доставки уменьшаются. Все товары с производств должны быть доставлены потребителям.

Потребности потребителей в товарах.

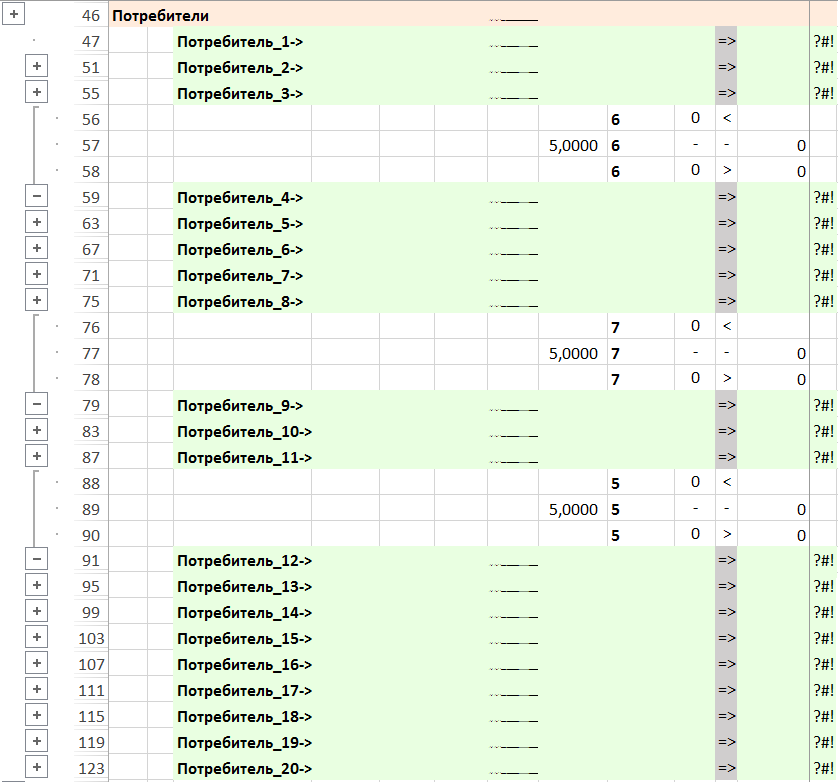
Рисунок. Фрагменты формы – стадия, емкость

Примечание. Все потребности потребителей в товарах удовлетворяются доставкой с производств.

кратко

Доставка товаров с производств потребителям

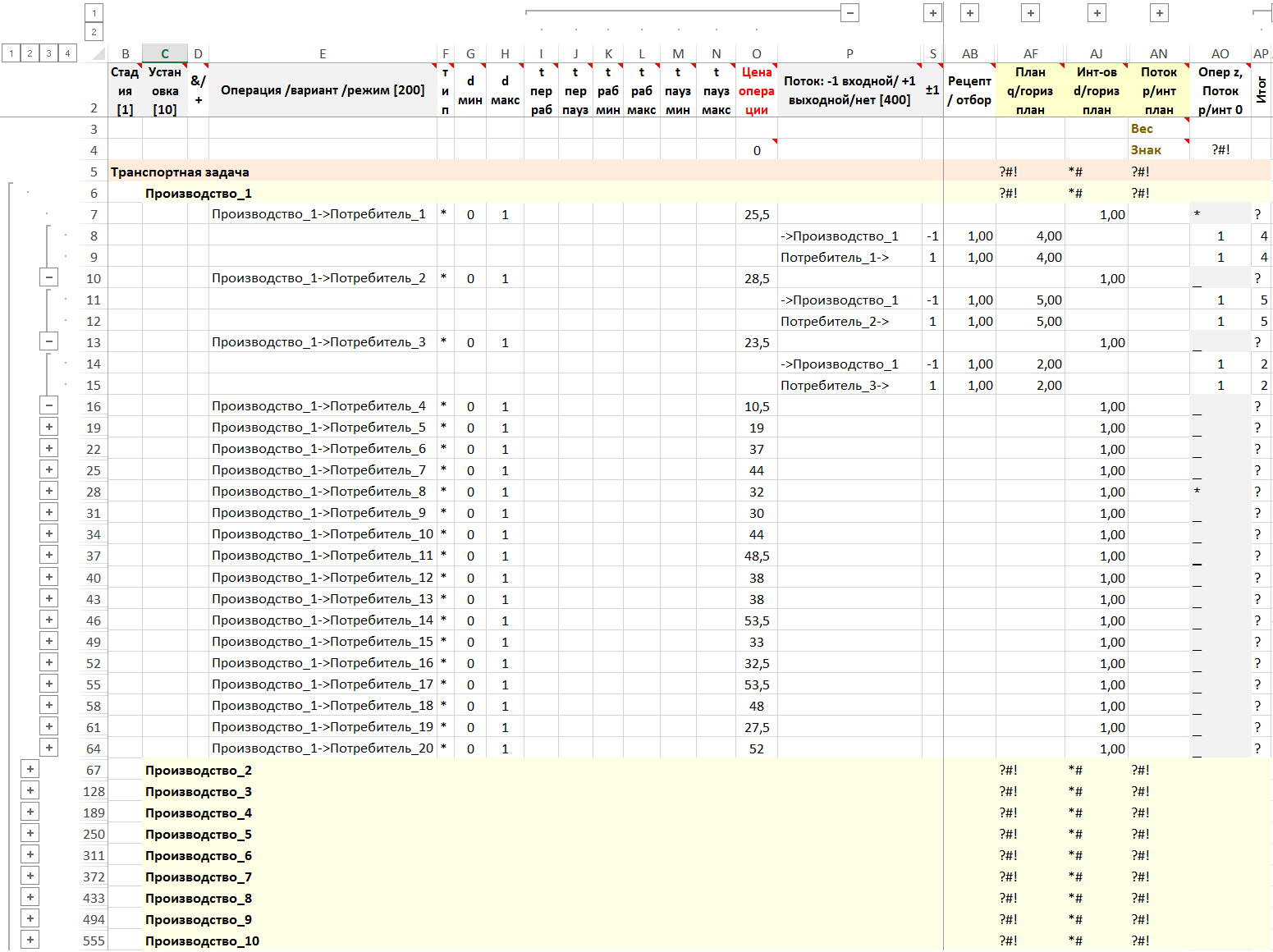
Рисунок. Фрагмент формы с результатами расчетов

Запасы производств и потребности потребителей:

Рисунок. Гистограммы изменения состояния емкостей

Объяснения решения

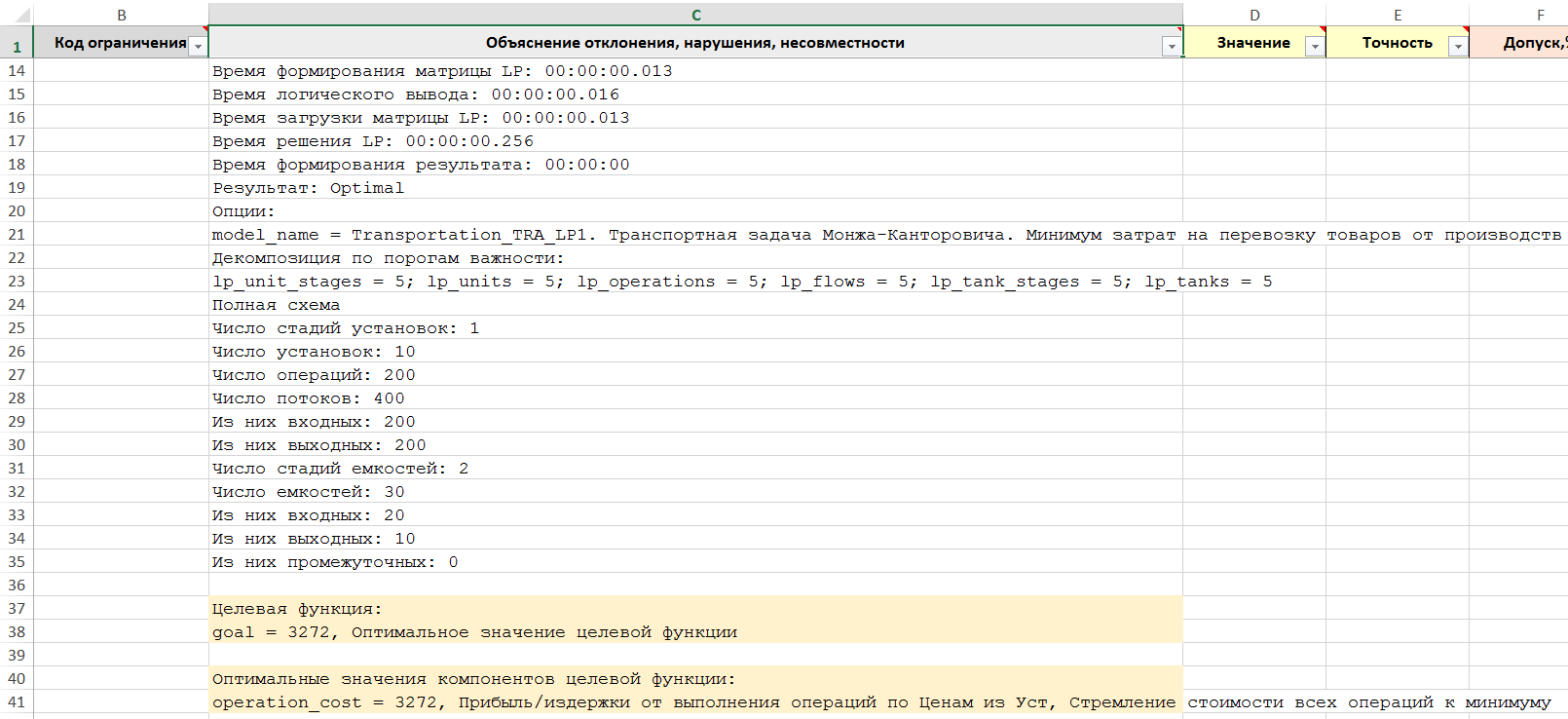
Рисунок. Фрагмент трассы объяснений Решателя LP

Размерность задачи и характеристики расчета

Размерность задачи:

Стадий 1, Установок 10, Операций 200, Емкостей 30, Интервалов 1, Переменных 1060, Ограничений 1524.

Характеристики расчета:

Минут до оптимального 00:00:00,256

Решатель LpSolve, сервер Intel Core i5-4570 3,2GHz.

кратко