Алеф-куб: как построить «умное» цифровое государство?
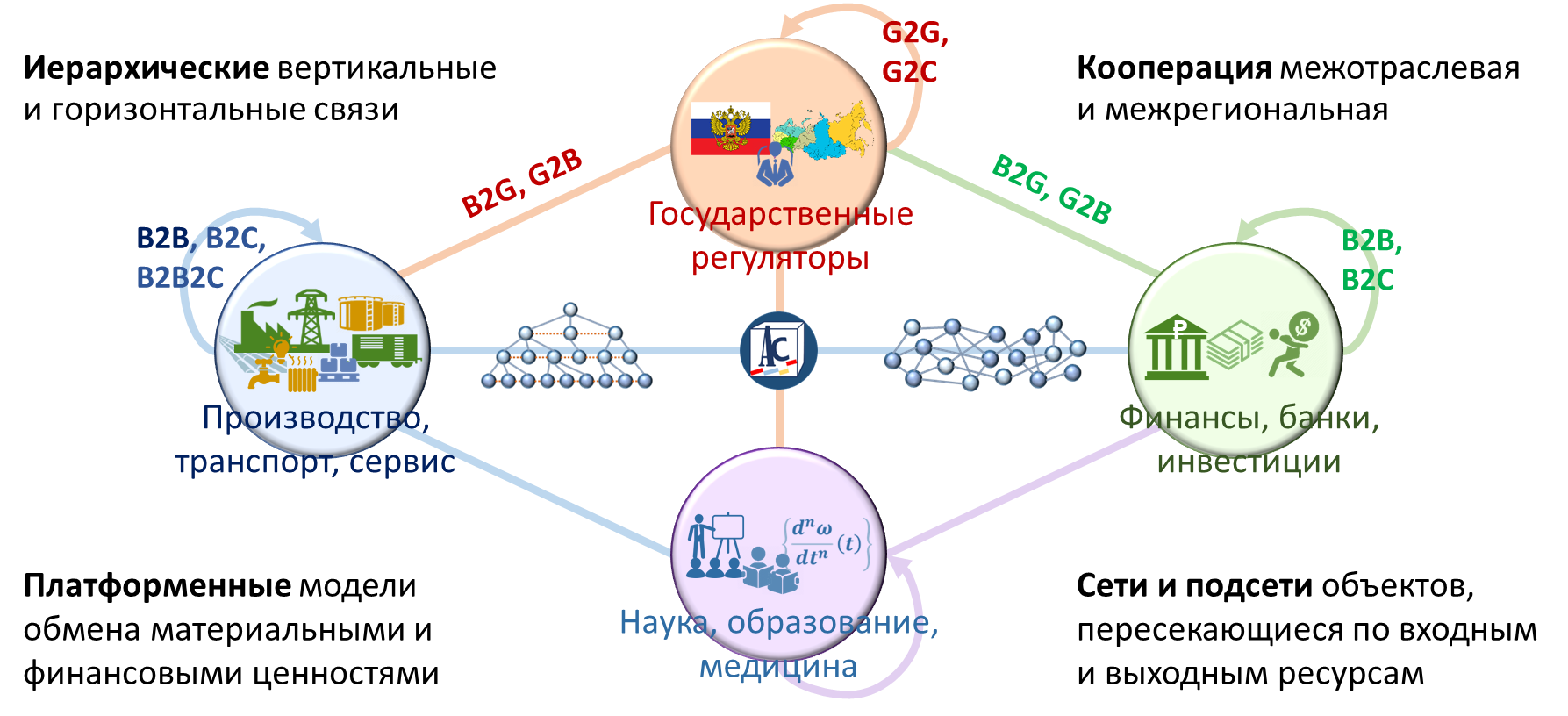
Соединить всех: бизнес, финансы, органы власти, науку, образование, медицину на Единой Платформе:
подробнее…
Алеф-куб: какое место занимает образование в нашей концепции?
Важное. Без образования не построить даже «умного» потребителя, тем более «умный» дом, город и страну.
кратко
Алеф-куб: в каком порядке строить? Дорожная карта
подробнее…
• Обеспечить «интеллектуальными двойниками» и оптимизировать предприятия бизнеса и их сетевое взаимодействие B2B.
• Добавить «мозги» ситуационным центрам регуляторов и органов власти, оптимизировать координацию их решений, включая межотраслевые и межрегиональные балансы G2G, и их взаимодействие с бизнесом B2G и G2B.
• Оснастить учебными и реальными моделями университеты и ВУЗы, научно-исследовательские и проектные институты.
• Построить кампусы и инновационные территориальные кластеры, включающие университеты, центры научных исследований и разработок, инженерные центры, бизнес-инкубаторы, технопарки, общественные организации, финансовые институты и пр.
• Переходить к «умному» городу B2C, G2C, региону, государству.

Эти этапы не обязательно проходить последовательно, их параллельная реализация и сетевое распространение быстрее дадут кумулятивный и синергетический эффект оптимизации и устойчивого развития экономики в целом.
Алеф-куб: почему актуальны проблемы образования?
По предыдущим шагам уже разработано множество типовых решений и шаблонов, их можно распространять прямо сейчас. Поэтому здесь рассмотрены в первую очередь университеты и кампусы.
кратко
Алеф-куб: кого обучаем?
Непрерывное образование на Единой Платформе включает профессиональное, дополнительное, корпоративное образование, в том числе обучение по работе на Платформе Алеф-куб.
подробнее…



кратко
Алеф-куб: в чем уникальность образовательных технологий?
Инструменты для обучения на Платформе Алеф-куб:
• Создание основного «содержания» курса — учебных моделей, документирование
подробнее…

кратко
• Создание и обновление учебных материалов, сохранение и передача знаний
подробнее…


кратко
• Поддержка учебного процесса и сервис
подробнее…


кратко
Алеф-куб: откуда брать модели для обучения?
Учеба, наука и жизнь на Платформе Алеф-куб 😊
подробнее…
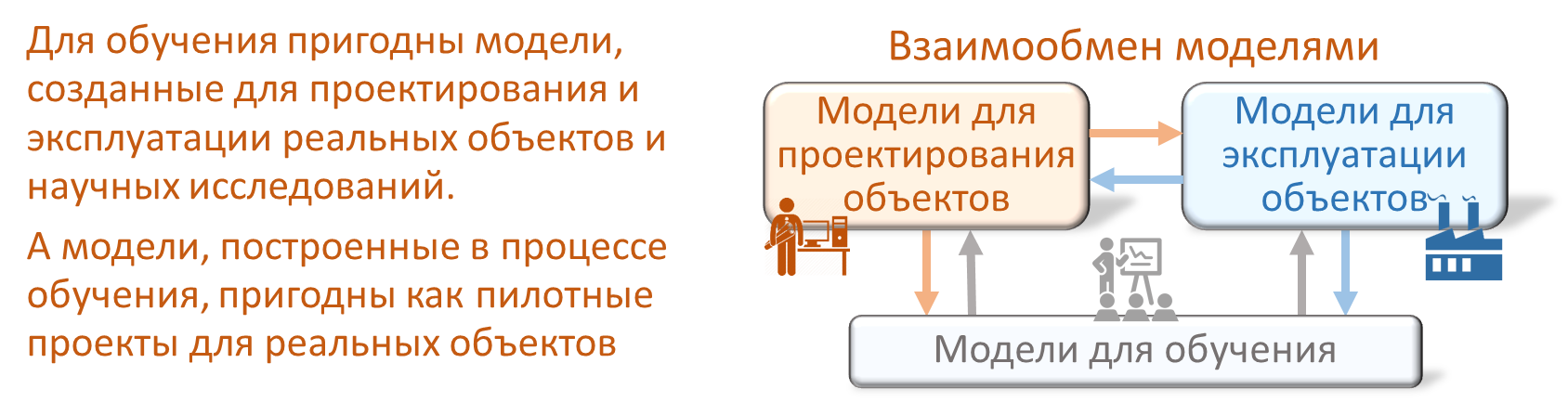

На сайте опубликованы порядка 200 типовых решений для разных областей, объектов, задач и бизнес-процессов. Все они пригодны для обучения.
кратко
Алеф-куб: как обучаем? Формы обучения.
подробнее…


кратко
Алеф-куб: технологии в образовании, что в них уникального?
подробнее…

кратко
Алеф-куб: другие вопросы и ответы
подробнее…


кратко
Технологии Алеф-куб в школе. EdTech.
Алеф-куб: как помочь школьнику?
Предложены технологические решения для сферы образования, EdTech (Education Technology).
Технологии Алеф-куб в школе могут научить школьника ставить задачи и создавать модели, это важнее, чем составлять уравнения, вычислять по формулам и решать абстрактные уравнения. Как это сделать? Школьные задачи можно получить как частные случаи единой модели планирования Алеф-куб.
подробнее…
Задачи школьного курса математики
Школьный курс математики включает разные типы задач:
• Вычисление , 1-4 класс, например, (5+2) 1,5=10,5. чисел. класс.
• Решение абстрактных уравнений и неравенств типа 3+2x=8, 3х <7, |3x−5| <3, систем линейных и уравнений и неравенств переменными, и др. решения. Решение способом . С , , и далее до и классов.
• Комбинаторные задачи. , класс и др.
• Множества и подмножества. и класс.
• Основы логики, алгебра высказываний и . — класс.
• , измерения , , , размерности. и действия над ними, точность погрешность измерения. класс.
• и интеграл. Корень n-ой степени. Степенные, показательные и логарифмические функции, уравнения и неравенства. Дифференцирование показательной и логарифмической функции. Графики функций и др. .
• Перевод условий задачи из словесной формы в формульную, уравнений, систем уравнений и , в том числе на , на скорость, на совместную работу, на проценты, доли и смеси и др. Задачи С 1 по 11 класс.
Обобщим эти задачи, выделив основные классы и сопоставив их с «недетскими» терминами, принятыми в Алеф-куб:
• Словесная постановка реальной прикладной задачи или «похожей» на реальную. Это обычно выполняют авторы учебников, задачников, пособий, реже – учителя.
• Создание математической модели, перевод условий задачи из словесной формы в формульную или комбинаторную.
• Решение задачи по модели, чаще всего в виде систем уравнений и неравенств, причем отдельными специальными приемами.
• Проверка решения подстановкой значений в формулы.
• Исследование решения, графическая иллюстрация и прочая «бизнес-аналитика».
Эти школьные задачи можно получить как частные случаи единой модели планирования, с одной стороны кажется, что это как стрелять из пушки по воробьям, но с другой стороны, виртуальную «пушку» не жалко, она от использования не обветшает и не износится.
Применение единой модели и решателя в школе с 1го класса поможет школьнику:
• научиться самостоятельно ставить задачи и создавать модели, пробовать разные способы описания и решения одной и той же задачи, и наоборот, придумывать содержательные задачи по уравнениям и неравенствам;
• развить наглядное и предметное представление задачи и процесса решения, воображение и навыки моделирования «в уме», применять «бизнес-аналитику» для исследования;
• почувствовать разницу между «подбором», проверкой решения (симуляция) и определением, поиском решения (оптимизация);
• увидеть, что математика – это не только числа, научиться пользоваться базовыми понятиями в широком смысле, такими как «время», «ресурс», «запас» (емкость), «действие» (операция), «движение», «скорость» (поток), «выбор» (установка) и др.
• в результате – воспринимать моделирование радостно и весело, как увлекательную игру.
Анализ и обобщение
В концепции единой модели Алеф-куб задачи по математике в начальных классах однотипны. Перечислим их отличия:
• количество «действий» (шагов, уравнений) для их решения;
• способ решения – подбор и подстановка значений (симуляция) или вычисление;
• требуется определить зависимые переменные или/и независимые или коэффициенты;
• используются (неявно) разные : пространственные (статика) или/и временные (динамика), порядковые (сравнение, неравенства, оптимизация) или шкалы наименований (выбор) и др., только натуральные числа или также отрицательные и дробные.
Пример задач в пространстве и во времени. У Оли было 10 яблок.
Статика. Она отдала 3 яблока Тане и еще 2 яблока Васе. Сколько яблок осталось у Оли?
Динамика. Она отдала сначала 3 яблока Тане, а потом еще 2 яблока Васе. Вопрос тот же.
На сайте приводятся примеры моделирования таких задач в Алеф-куб по возрастанию сложности.
кратко
Алеф-куб: как помочь школьному учителю?
Подготовка серий задач с помощью инструментов Алеф-куб.
