PRSchoolCrows_PRA_DP3Opt02-04. Уроки моделирования на задачах начальной школы. Считаем ворон. Практические задания. 3 шага. Прилетели 10 ворон, улетели 3, потом 2. Без учета переключений.

•  Задачи рекомендуется изучать в порядке возрастания сложности, поскольку в следующих задачах, как правило, не повторяются пояснения к предыдущим, а приводится ссылка и вводятся новые инструменты моделирования. В некоторых решениях «наследуется» полностью модель и схема объекта, но изменяется, например, горизонт планирования, ограничения или критерии.

•  Нумерация объектов и задач может содержать пропуски, оставленные для развития темы и для самостоятельных практических работ.

•  Сравнивать задачи и решения как из одной, так и из разных серий удобно в нескольких вкладках браузера, «вытащив» их в отдельные окна.

•  Некоторые решения опираются не на самую удачную модель, они предполагают самостоятельную практическую работу по улучшению модели.

кратко

В концепции единой модели Алеф-куб задачи по математике в начальных классах в основном однотипны. Перечислим их отличия:

•  количество «действий» (шагов, уравнений) для их решения;

•  способ решения – подбор и подстановка значений (симуляция) или вычисление;

•  требуется определить зависимые переменные или/и независимые или коэффициенты;

•  используются (неявно) разные : пространственные (статика) или/и временные (динамика), порядковые (сравнение, неравенства, оптимизация) или шкалы наименований (выбор) и др., только натуральные числа или также отрицательные и дробные.

кратко

Сравним базовые задачи из учебника для 1 класса.

1 класс. Реши задачу.

«Считаем ворон». Дано: Прилетели 10 ворон и сели на ветку. Сначала улетело 3 вороны, а потом улетело ещё 2 вороны. Определить: Сколько ворон на ветке?

«У Оли яблоки». Дано: Оле дали 10 яблок.

«Оля съела все». Оля сама съела сначала 3, потом еще 2. Определить: Сколько яблок у Оли?

«Оля угостила». Оля сначала отдала 3 яблока Тане, а потом еще 2 яблока Васе. Определить: Сколько яблок у Оли?

Общее у всех этих задач:

•  Все эти задачи – динамические, календарного планирования, описывают процесс и в пространстве, и во времени. Статическая модель не адекватна постановке задач: все 2+3=5 ворон должны улететь сразу, а Оле придется в один присест съесть все 2+3=5 яблок, что не реально, или мгновенно отдать их сразу двоим, хотя 5 яблок не поместятся в руке.

•  Все эти задачи описывает одна и та же схема математической модели, математически это одна базовая модель, но с разным вербальным описанием, из разных предметных областей.

Рисунок. Схемы объекта для трех задач, сгенерированные автоматически

Отличия задач «У Оли яблоки» от задачи «Считаем ворон»:

•  Терминология, предметная область – орнитология (изучает птиц) и педагогика (или этика – яблоками нужно делиться), словесная постановка.

•  Число ворон может быть только целым, – это дискретная (целочисленная) переменная, число яблок – непрерывная переменная, съесть можно и часть яблока, и угостить можно, например, половиной или третью.

•  Число ворон – наблюдаемые переменные, число яблок – переменные, управляемые Олей.

Отличие задач «Съела» от задач «Угостила» и «Вороны»:

•  Если Оля съела яблоки, их невозможно вернуть, а если угостила, ей могут их вернуть. И вороны могут вернуться обратно на ветку.

Еще две подобных задачи.

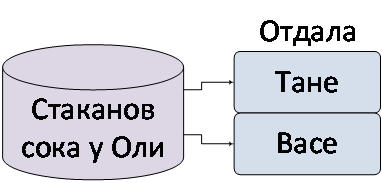
«Сок». Дано: Оля выжала 10 стаканов сока. Сначала она отдала 3 стакана Тане, а потом отдала еще 2 стакана Васе. Определить: Сколько стаканов сока осталось у Оли?

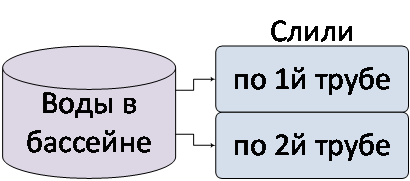
«Бассейн». Дано: В бассейне было 100 куб. метров воды. Сначала слили 30 куб. метров по 1й трубе, потом еще 20 куб. метров по 2й трубе. Определить: Сколько воды осталось в бассейне?

Их модели аналогичны предыдущим.

Выводы. Анализ показывает:

•  Общность, абстрактность и единство математических моделей для разных предметных областей, в данном случае орнитологии (раздел зоологии, изучающий птиц) и педагогики (яблоками нужно делиться).

•  Различие между вербальным (словесным) и формальным математическим описанием задачи.

•  Основой моделей даже таких «детских» задач являются ресурсы – вороны, яблоки и др., потоки – движение ресурсов, операции – действия с ресурсами, балансы ресурсов – законы сохранения, а также явно или неявно присутствуют цели.

•  Направления и характеристики, по которым нужно исследовать задачу для моделирования (тип ресурса и балансов, характер операций, шкалы и др.).

•  Как использовать типовые решения из одной предметной области для, казалось бы, совсем другой области.

кратко

Постановка базовой задачи

1 класс. Реши задачу.

Дано: Прилетели 10 ворон и сели на ветку. Сначала улетело 3 вороны, а потом улетело ещё 2 вороны.

Определить: Сколько ворон на ветке?

Особенности.

•  Схема объекта включает всего одну установку и одну емкость.

•  Число ворон может быть только целым.

•  Задача динамическая, календарного планирования, при постановке задачи в статике 2+3=5 ворон должны улететь сразу, в этом мало смысла.

кратко

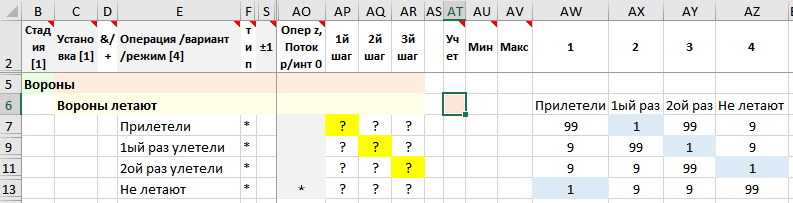
Рисунок. Фрагмент формы – матрица переходов при выборе 3го уровня иерархии элементов

Лист емкостей – тот же

На листе опций – Горизонт планирования– тот же, 3 интервала на горизонте

кратко

Объяснения решения

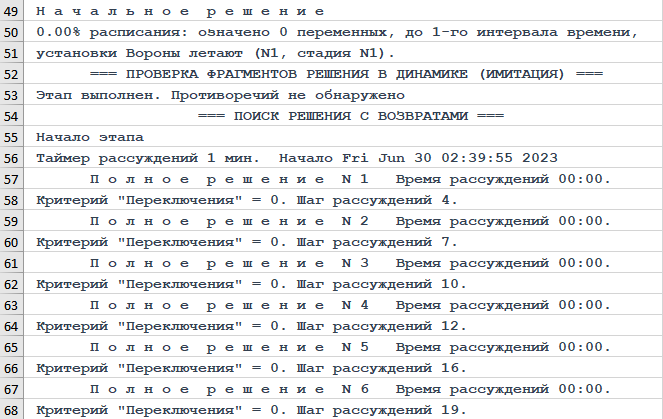
Рисунок. Начало трассы объяснений хода рассуждений Решателя DP

…

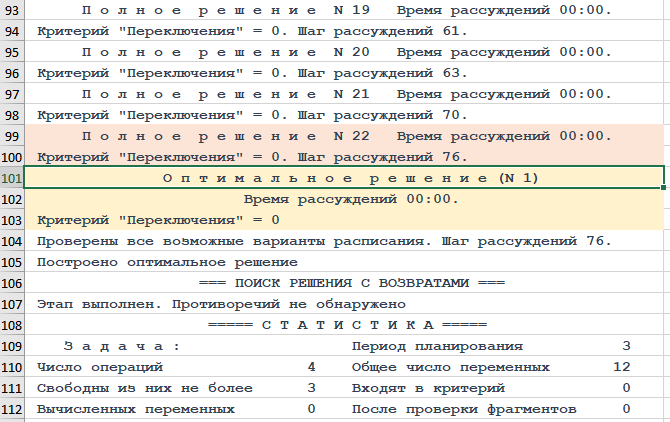
Рисунок. Фрагмент трассы объяснений хода рассуждений Решателя DP

кратко