GraphColor_PLN_DP1. Раскраска графа. Минимум цветов, соседние вершины графа разного цвета. Объемное агрегированное планирование. 1 интервал. * В процессе оформления.

Постановка задачи

В теории графов раскраска графов является частным случаем разметки графов. При раскраске элементам графа ставятся в соответствие метки с учётом определенных ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин.

Дано:

•  Неориентированный граф с вершинами и ребрами.

•  Набор цветов, в которые могут быть окрашены вершины графа. Верхняя оценка равна максимальной степени вершин графа + 1 (оценка жадного алгоритма).

Требуется:

Найти раскраску вершин графа минимальным числом цветов так, чтобы соседние вершины имели разный цвет.

кратко

Описывается раскраска графа

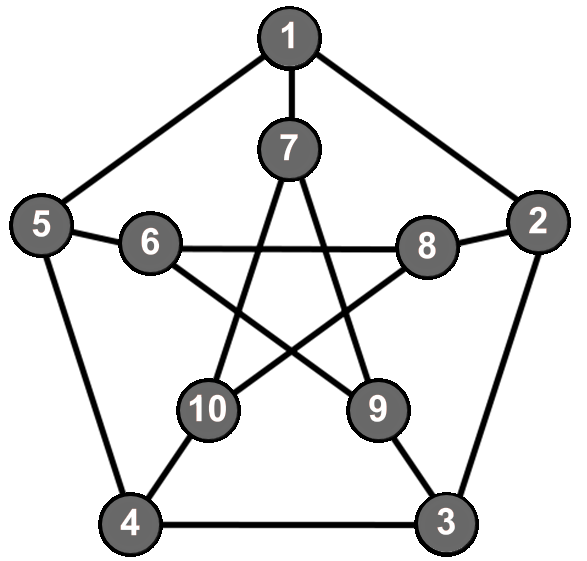
Рисунок. Исходный граф для раскраски

Число установок соответствует числу вершин графа. Дополнительные установки, соответствующие числу цветов для подсчитывания общего числа использованных цветов для раскраски:

Установки первой группы отражают покраску вершины графа в один из цветов.

Операции установок первой группы – покраска вершины в определенный цвет. Потоки операций отсутствуют.

Установки второй группы отражают использование цвета для окраски вершин графа.

Операции установок второй группы – использование и неиспользование цвета для раскраски вершин графа. Потоки операций отсутствуют.

кратко

Установки первого типа

Рисунок. фрагмент потоковой схемы объекта «с именами»

Установки второго типа

Рисунок. фрагмент потоковой схемы объекта «с именами»

кратко

Учитывается ограничения:

Ограничение на разный цвет соседних вершин, который задается через ограничение на альтернативности операций. Для каждого ребра устанавливается альтернативность покраски соединяемых вершин в один цвет.

Задается построением модели – альтернативностью операций установки

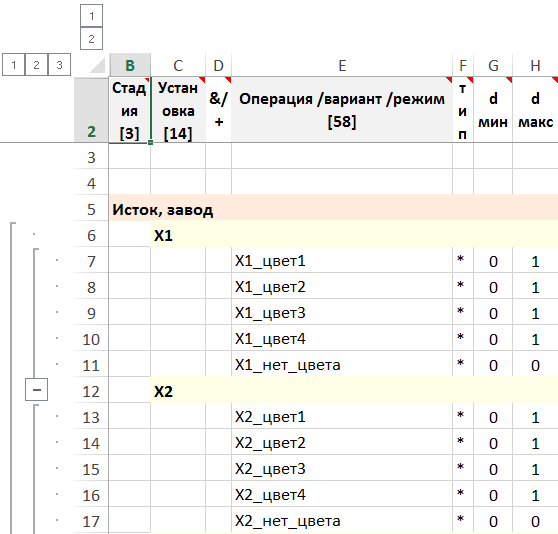
Рисунок. Фрагмент формы – стадия, установка, операция, поток

Связь между использованием цвета для окраски вершин графа (операций установки второй группы) и выбранным цветом покраски вершины (операций установок первой группы) задается ограничениями на одновременную работу и паузу операций.

Связь между используемым цветом и поркаской вершин

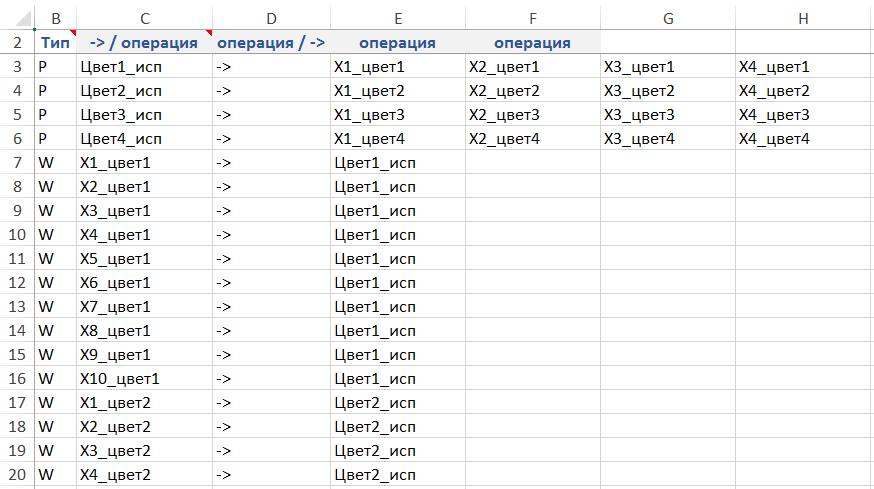
Рисунок. Фрагмент формы – ограничения на операции в интервалах времени

Критерий – минимум использованных цветов для покраски вершин графа. Для минимизации количества использованных цветов используется критерий «Выполнение». Для этого цена операций использования цвета для покраски вершин графа равна 1, значение критерия отражает число использованных цветов.

Цены операций для определения числа использованных цветов

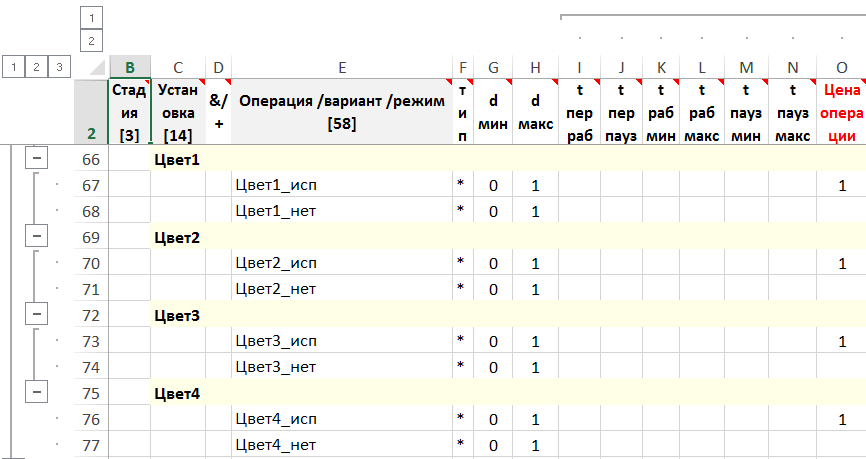
Рисунок. Фрагмент формы – стадия, установка, операция, поток

кратко

Вершины графа и используемые цвета для раскраски

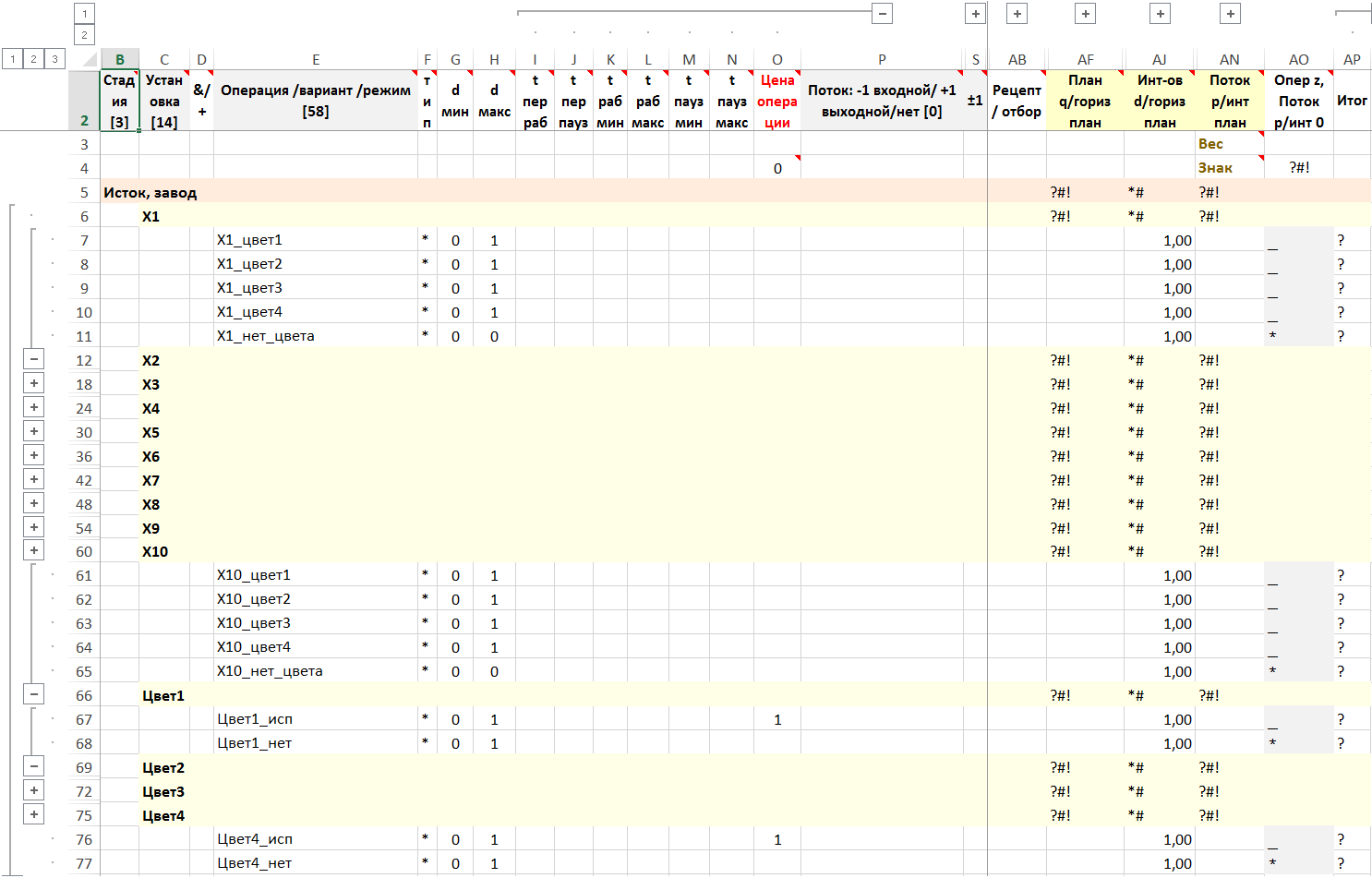
Рисунок. Фрагмент формы – стадия, установка, операция, поток

кратко

Фрагменты расписания

Окраска вершин 1 — 5

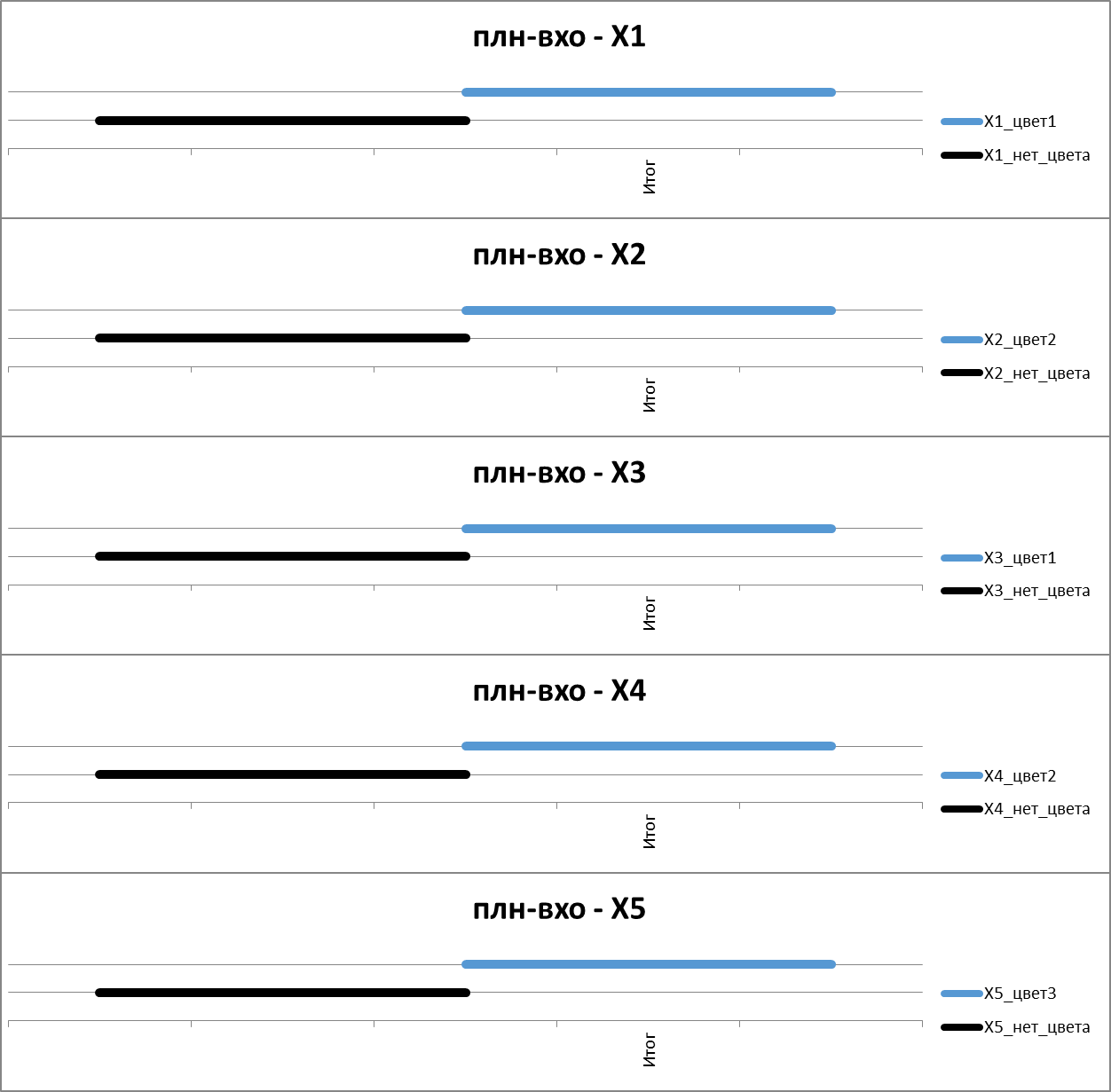
Рисунок. Фрагмент расписания выполнения операций

Окраска вершин 6 — 10

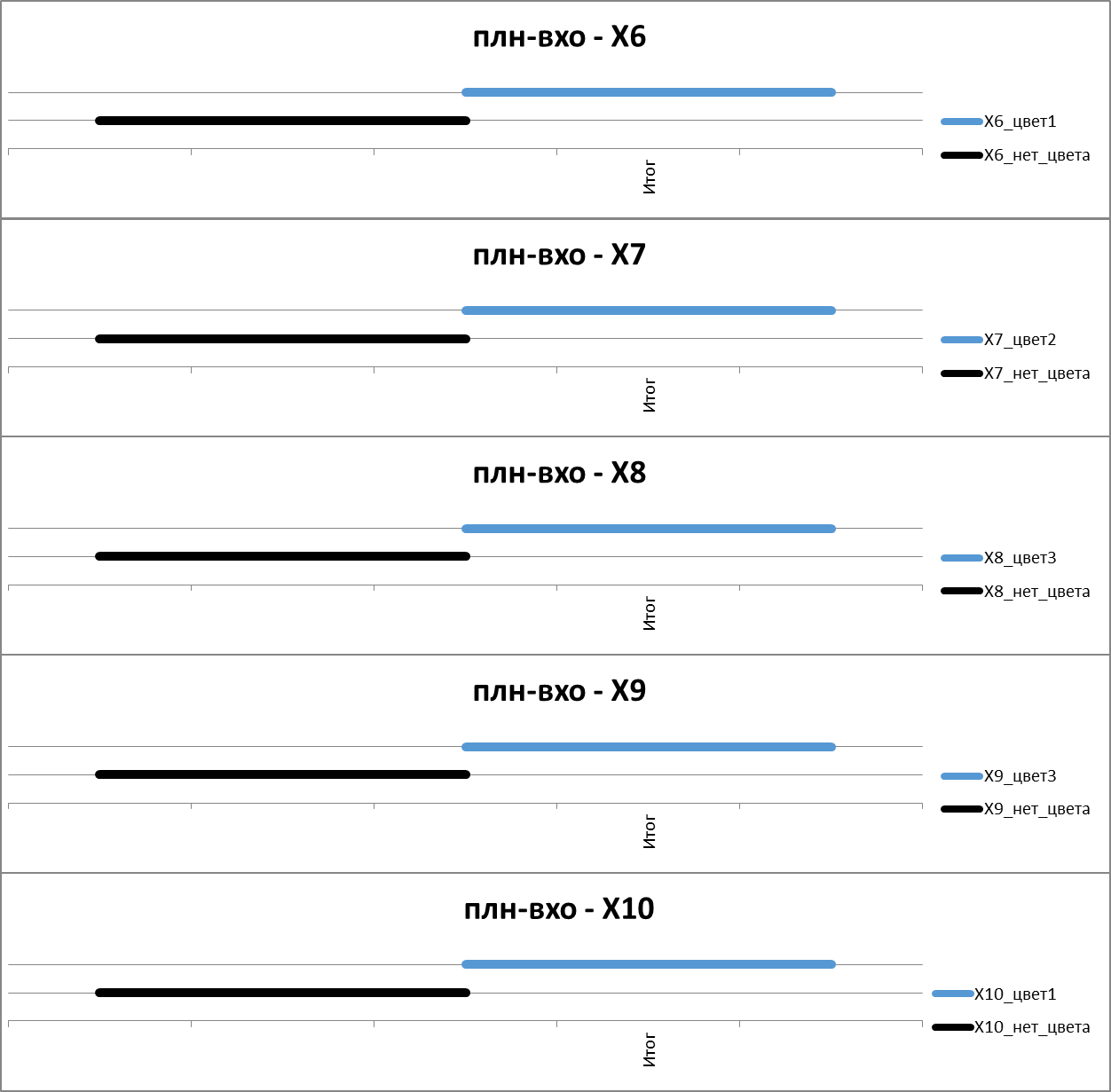
Рисунок. Фрагмент расписания выполнения операций

Использование цветов

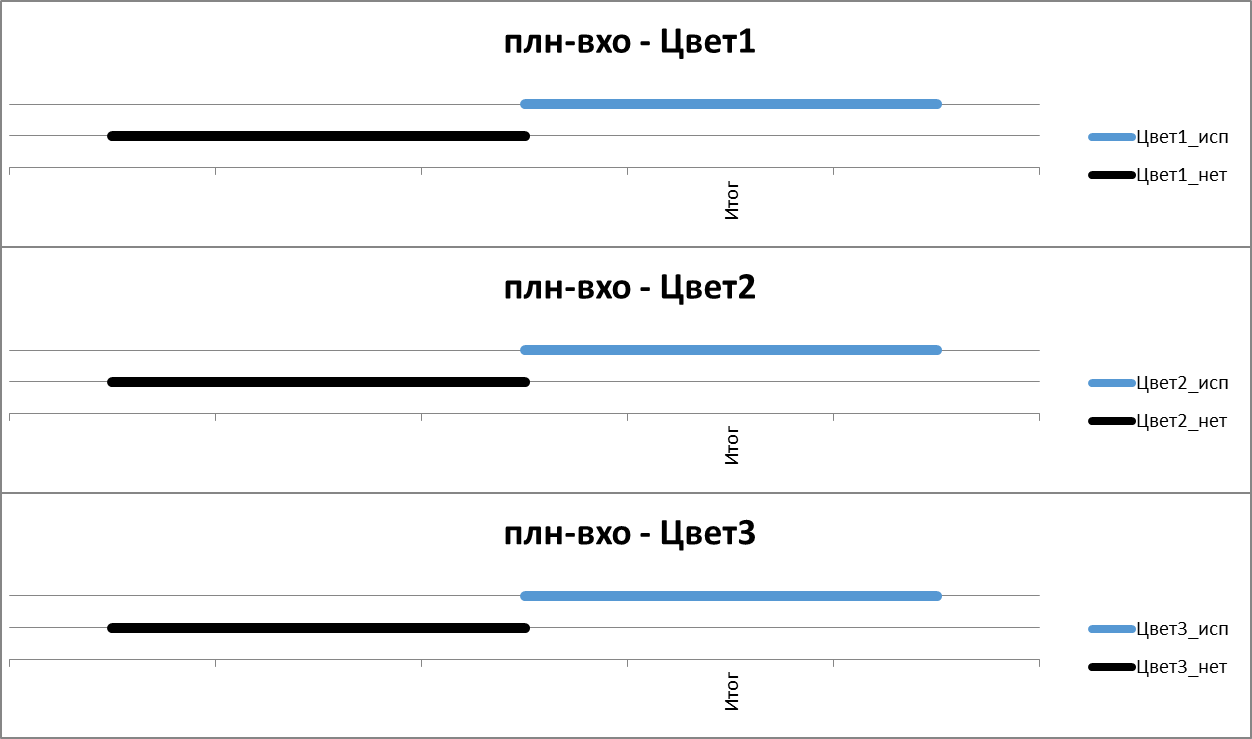
Рисунок. Фрагмент расписания выполнения операций

Объяснения решения

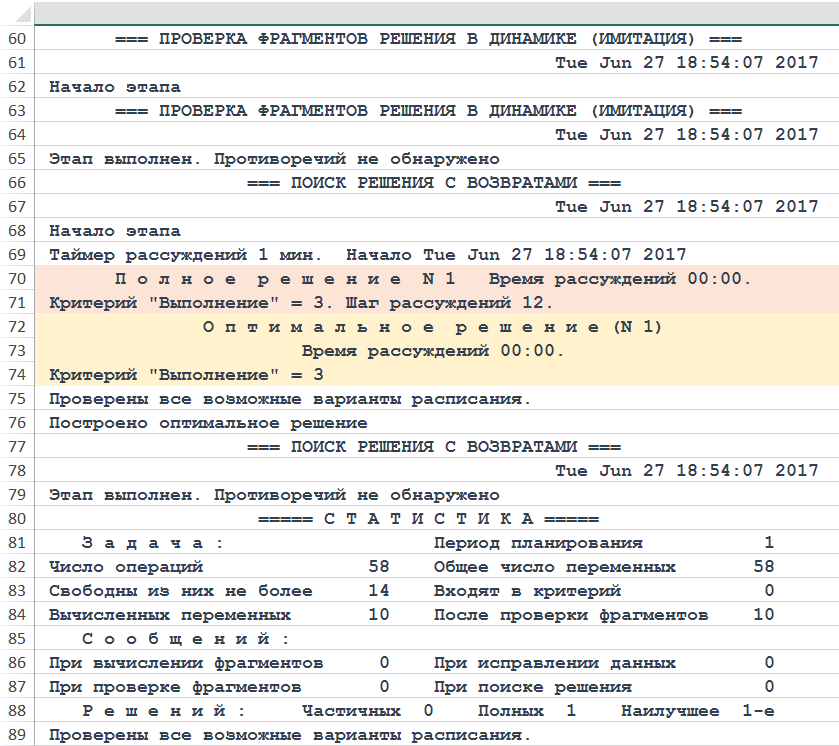
Рисунок. Фрагмент трассы объяснений хода рассуждений Решателя DP

Размерность задачи и характеристики расчета

Размерность задачи:

Стадий 1, Установок 14, Операций 58, Емкостей 0, Интервалов 1, Переменных 58.

Характеристики расчета:

Частичных решений 0; Полных решений 1; Оптимальных решений 1;

Шагов до 1го полного 12; до наилучшего полного 12;

Минут до 1го полного 00:00; до наилучшего полного 00:00; до оптимального 00:00;

Решатель операций KS3, сервер Intel Core i5-4570 3,2GHz.

кратко