BinPackingBin_SCH_DP7. Упаковка в контейнеры. Минимум контейнеров, загрузка контейнеров предметами. Календарное планирование. 7 предметов.

Постановка задачи

Задача об упаковке в контейнеры – NP-трудная комбинаторная задача. Задача заключается в упаковке объектов предопределённой формы в конечное число контейнеров предопределённой формы таким способом, чтобы число использованных контейнеров было наименьшим или количество, или объём объектов (которые упаковывают) были наибольшими.

Дано:

•  Набор предметов предопределенной формы для упаковки в контейнеры.

•  Набор контейнеров заданного объема, которые можно использовать для упаковки.

Требуется:

Найти число заполненных контейнеров и их упаковку предметами, чтобы их количество было минимальным.

кратко

Число установок соответствует максимально возможному числу контейнеров, т.е. числу вещей – предельный случай, когда каждый предмет пакуется в отдельный контейнер.

Число интервалов равно числу вещей, т.е. в каждый момент упаковывается одна из вещей.

Установки отражают заполнение контейнера предметами. Операция установки типа «Предмет->К*» – положить предмет в контейнер. Загружаемый в контейнер предмет определяется интервалом. Операции этого типа для разных контейнеров являются альтернативными. Потоками операции «Предмет->К*» являются характеристики (объем) предмета, который пакуется в один из контейнеров и счетчик числа предметов, характеризующий потребность в упаковке предмета. В каждый интервал времени упаковывается один предмет, чьи характеристики (объем и счетчик) задаются в значениях потоков.

Операция установки «К*_занят» – в контейнер в данном интервале не упаковываются предметы, но контейнер уже занят.

Операция установки «К*_свободен» – в контейнер в данном интервале не упаковываются предметы, и контейнер свободен. Переход с этой операции не возможен на операцию «К*_занят». Кроме того, запрещен переход на данную операцию со всех остальных операций. Задаются ограничениями на длительности выполнения/паузы операций от начала/конца другой.

Критерий – минимум числа занятых контейнеров. Для минимизации числа используемых контейнеров используется критерий «Переключение». В матрице переключений операций стоимость перехода с операции «К*_свободен» на другие равна 1. Переходы других операций не регулируются, стоимости переходов равны 0. Этот критерий не регулирует ни заполнение контейнеров, ни количество свободного места в них.

кратко

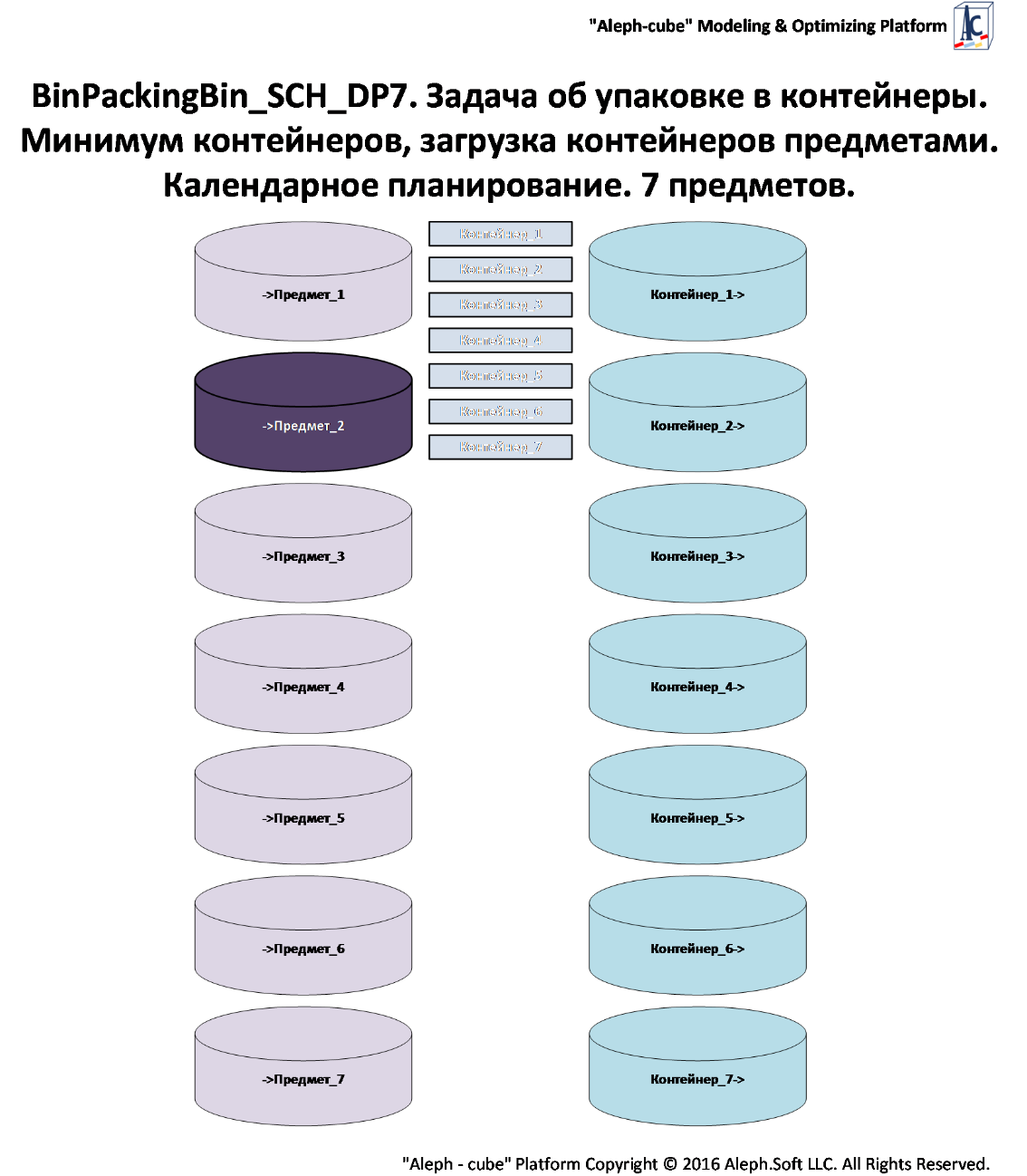
Рисунок. Общий вид потоковой схемы объекта «краткая»

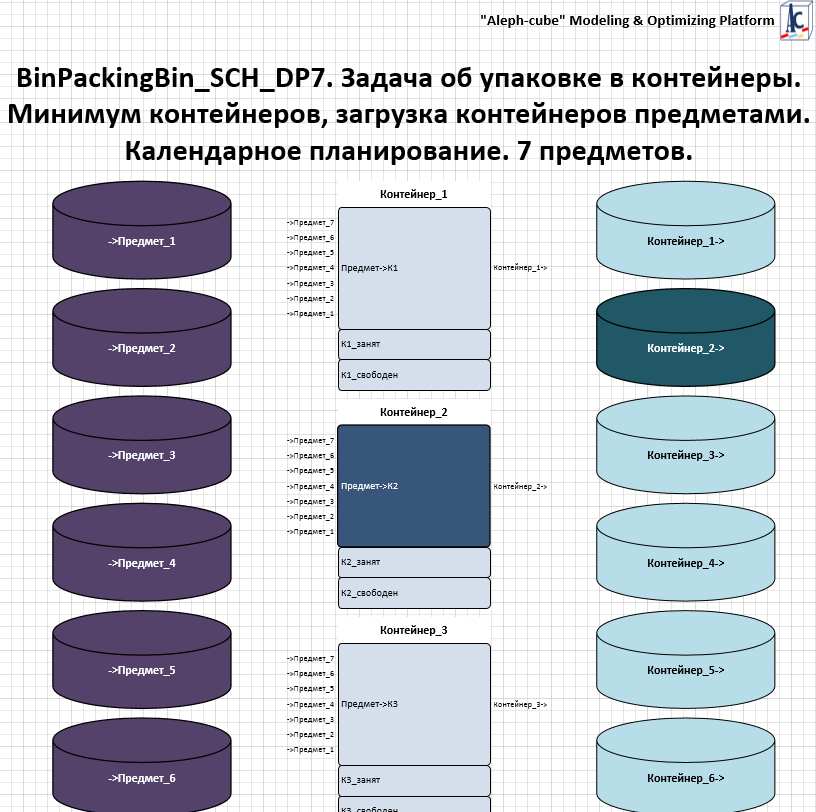
Рисунок. фрагмент потоковой схемы объекта «с именами»

кратко

Минимизация числа контейнеров для упаковки 7 предметов.

Объем занимаемого места предметов, пакуемых в контейнер: Предмет1 – 2 куб.м., Предмет2 – 5 куб.м., Предмет3 – 4 куб.м., Предмет4 – 7 куб.м., Предмет5 – 1 куб.м., Предмет6 – 3 куб.м., Предмет7 – 8 куб.м.

Состояние контейнеров и переходы между ними

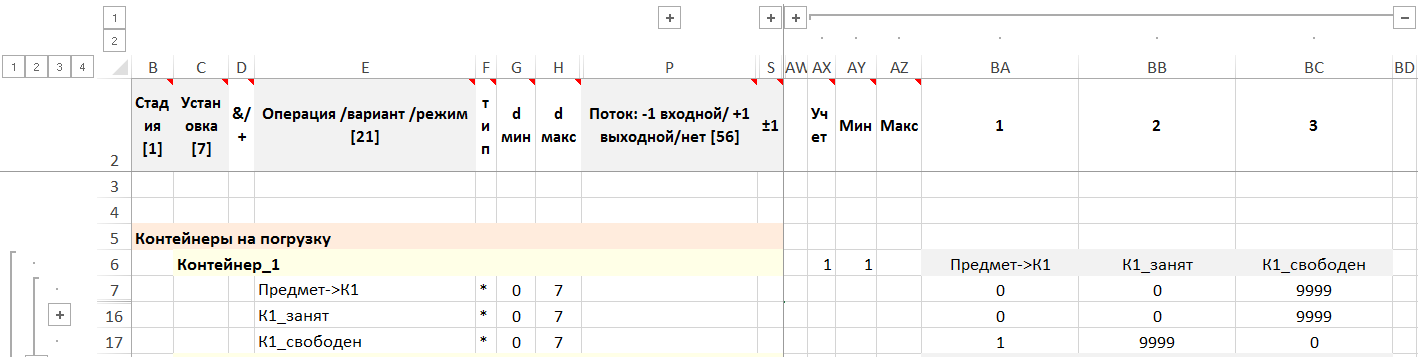
Рисунок. Фрагмент формы – матрица переналадок

кратко

Контейнеры для упаковки предметов

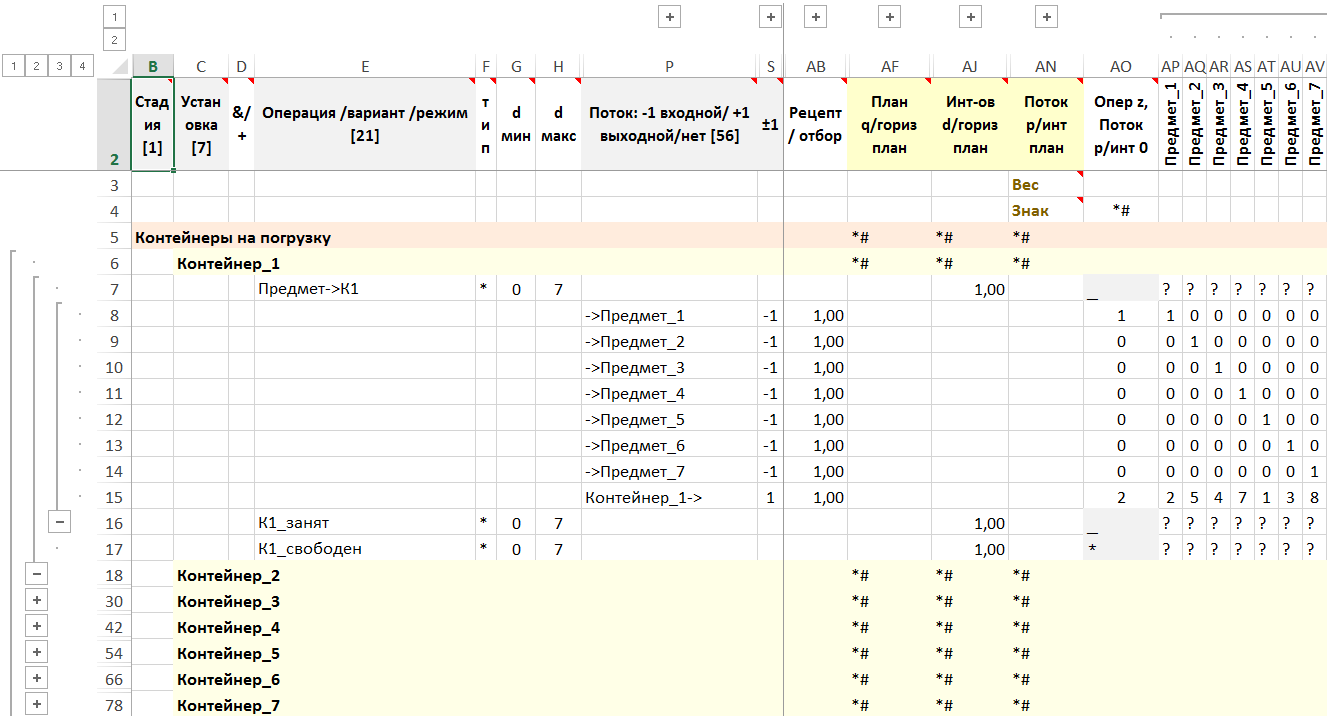
Рисунок. Фрагмент формы – стадия, установка, операция, поток

Примечание. Видны интервалы времени и потоки, моделирующие результат упаковки предмета в контейнер – занятие объема контейнера и счетчик упаковки предмета.

Невозможность упаковки одного и того же предмета в разные контейнерызадана альтернативностью в ограничениях на операции:

Рисунок. Ограничения на операции в интервалах времени

Невозможные переходы состояния контейнеров запрещены в ограничених на работу или паузу одной операции от начала или конца другой:

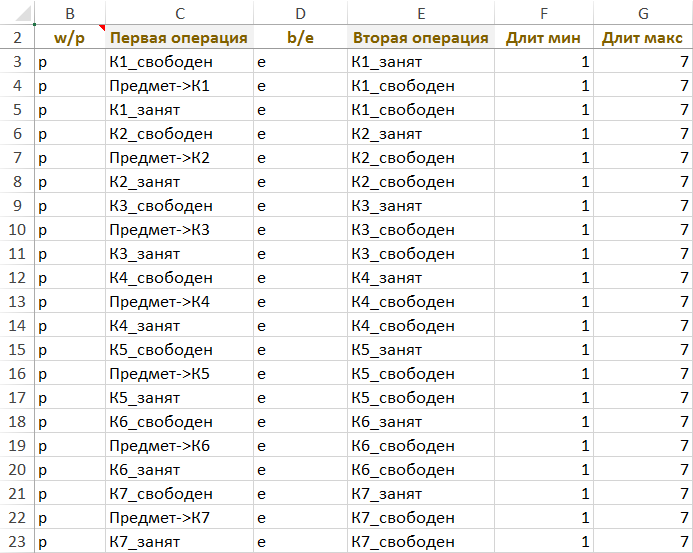
Рисунок. Ограничения на работу или паузу одной операции от начала или конца другой

кратко

Фрагменты расписания

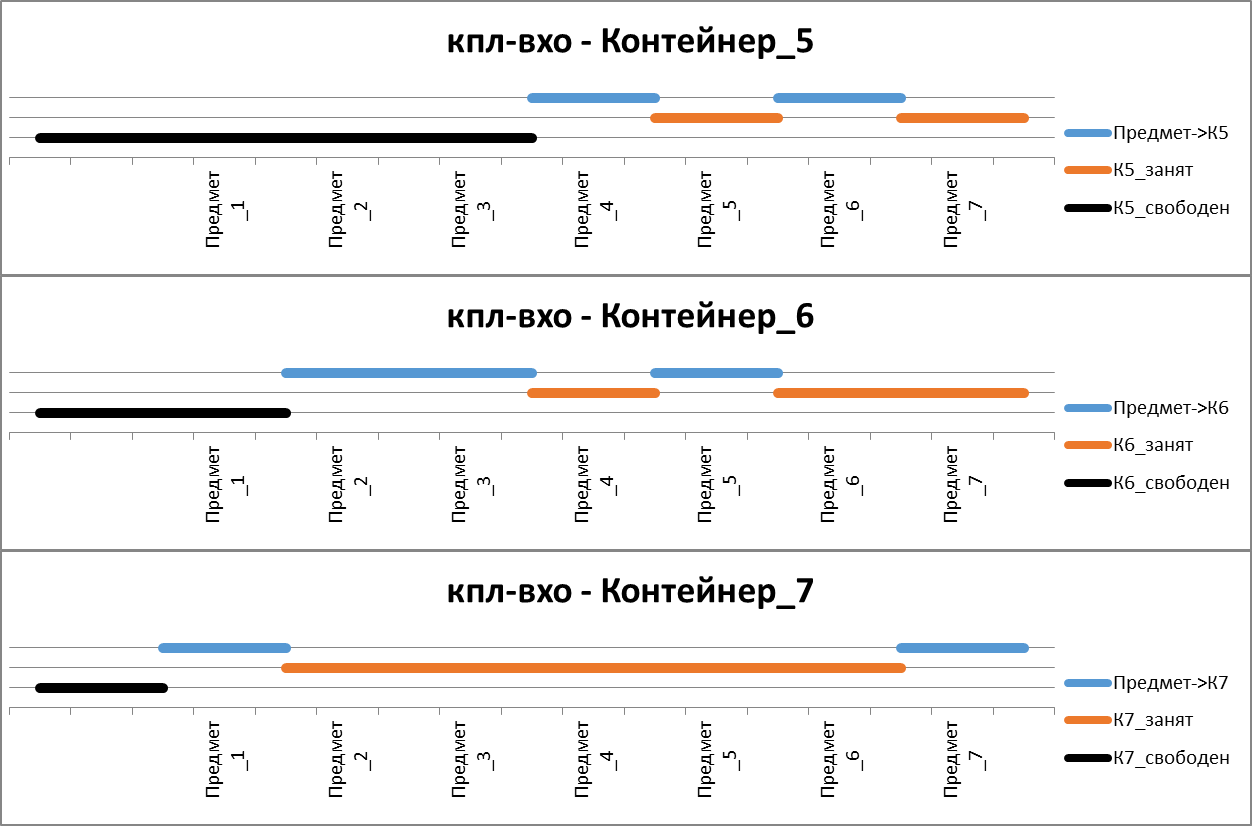
Рисунок. Фрагмент расписания выполнения операций

Упаковка предметов в контейнеры и занимаемый ими объем:

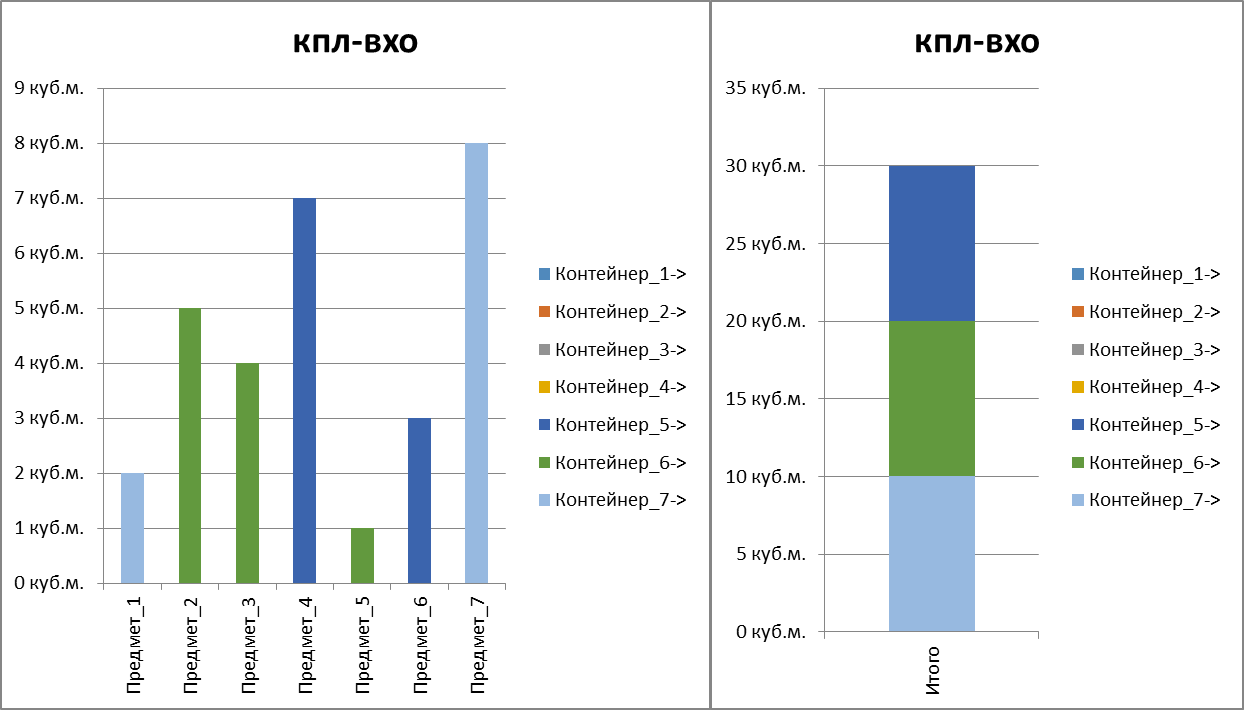
Рисунок. Гистограммы изменения состояния емкостей

Объяснения решения

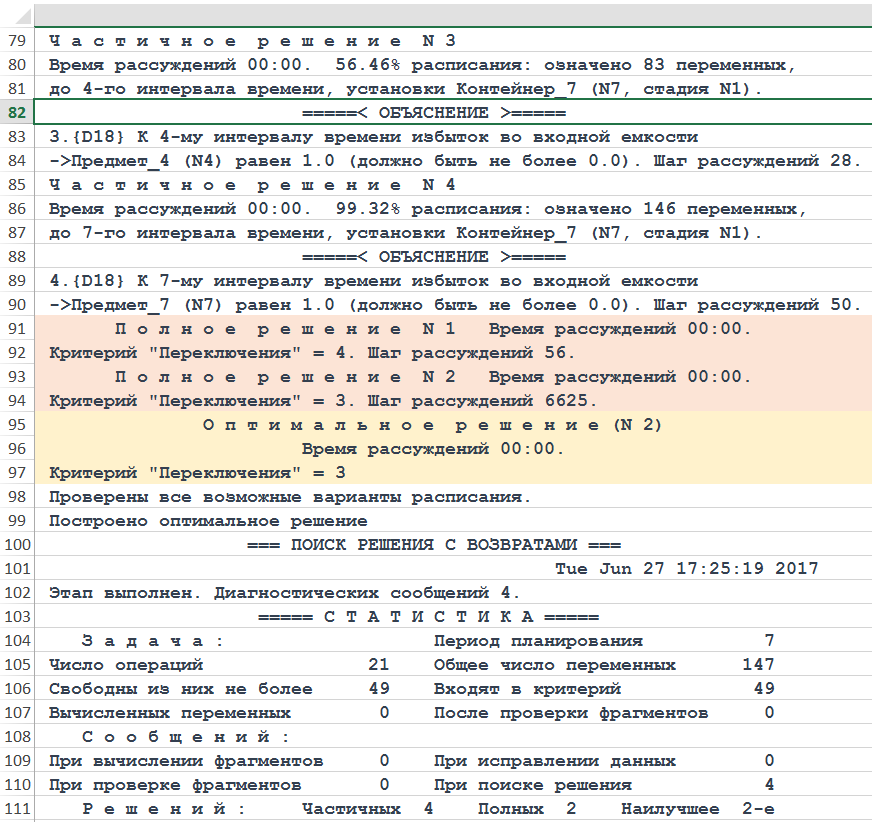
Рисунок. Фрагмент трассы объяснений хода рассуждений Решателя DP

кратко