PRSchoolApples_PRA_DP2Sim01-00. Уроки моделирования на задачах начальной школы. У Оли яблоки. Практические задания. 2 шага. У Оли было 10 яблок. Съела сама 3, потом еще 2. Сколько осталось?

•  Задачи рекомендуется изучать в порядке возрастания сложности, поскольку в следующих задачах, как правило, не повторяются пояснения к предыдущим, а приводится ссылка и вводятся новые инструменты моделирования. В некоторых решениях «наследуется» полностью модель и схема объекта, но изменяется, например, горизонт планирования, ограничения или критерии.

•  Нумерация объектов и задач может содержать пропуски, оставленные для развития темы и для самостоятельных практических работ.

•  Сравнивать задачи и решения как из одной, так и из разных серий удобно в нескольких вкладках браузера, «вытащив» их в отдельные окна.

•  Некоторые решения опираются не на самую удачную модель, они предполагают самостоятельную практическую работу по улучшению модели.

кратко

В концепции единой модели Алеф-куб задачи по математике в начальных классах в основном однотипны. Перечислим их отличия:

•  количество «действий» (шагов, уравнений) для их решения;

•  способ решения – подбор и подстановка значений (симуляция) или вычисление;

•  требуется определить зависимые переменные или/и независимые или коэффициенты;

•  используются (неявно) разные : пространственные (статика) или/и временные (динамика), порядковые (сравнение, неравенства, оптимизация) или шкалы наименований (выбор) и др., только натуральные числа или также отрицательные и дробные.

кратко

Сравним базовые задачи из учебника для 1 класса.

1 класс. Реши задачу.

«Считаем ворон». Дано: Прилетели 10 ворон и сели на ветку. Сначала улетело 3 вороны, а потом улетело ещё 2 вороны. Определить: Сколько ворон на ветке?

«У Оли яблоки». Дано: Оле дали 10 яблок.

«Оля съела все». Оля сама съела сначала 3, потом еще 2. Определить: Сколько яблок у Оли?

«Оля угостила». Оля сначала отдала 3 яблока Тане, а потом еще 2 яблока Васе. Определить: Сколько яблок у Оли?

Общее у всех этих задач:

•  Все эти задачи – динамические, календарного планирования, описывают процесс и в пространстве, и во времени. Статическая модель не адекватна постановке задач: все 2+3=5 ворон должны улететь сразу, а Оле придется в один присест съесть все 2+3=5 яблок, что не реально, или мгновенно отдать их сразу двоим, хотя 5 яблок не поместятся в руке.

•  Все эти задачи описывает одна и та же схема математической модели, математически это одна базовая модель, но с разным вербальным описанием, из разных предметных областей.

Рисунок. Схемы объекта для трех задач, сгенерированные автоматически

Отличия задач «У Оли яблоки» от задачи «Считаем ворон»:

•  Терминология, предметная область – орнитология (изучает птиц) и педагогика (или этика – яблоками нужно делиться), словесная постановка.

•  Число ворон может быть только целым, – это дискретная (целочисленная) переменная, число яблок – непрерывная переменная, съесть можно и часть яблока, и угостить можно, например, половиной или третью.

•  Число ворон – наблюдаемые переменные, число яблок – переменные, управляемые Олей.

Отличие задач «Съела» от задач «Угостила» и «Вороны»:

•  Если Оля съела яблоки, их невозможно вернуть, а если угостила, ей могут их вернуть. И вороны могут вернуться обратно на ветку.

Еще две подобных задачи.

«Сок». Дано: Оля выжала 10 стаканов сока. Сначала она отдала 3 стакана Тане, а потом отдала еще 2 стакана Васе. Определить: Сколько стаканов сока осталось у Оли?

«Бассейн». Дано: В бассейне было 100 куб. метров воды. Сначала слили 30 куб. метров по 1й трубе, потом еще 20 куб. метров по 2й трубе. Определить: Сколько воды осталось в бассейне?

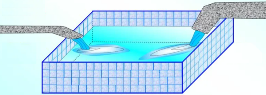
Их модели аналогичны предыдущим.

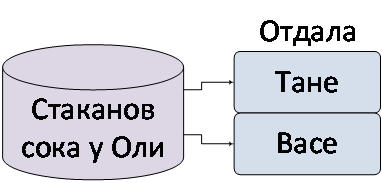
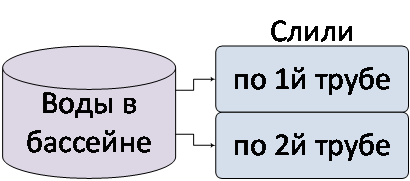
Выводы. Анализ показывает:

•  Общность, абстрактность и единство математических моделей для разных предметных областей, в данном случае орнитологии (раздел зоологии, изучающий птиц) и педагогики (яблоками нужно делиться).

•  Различие между вербальным (словесным) и формальным математическим описанием задачи.

•  Основой моделей даже таких «детских» задач являются ресурсы – вороны, яблоки и др., потоки – движение ресурсов, операции – действия с ресурсами, балансы ресурсов – законы сохранения, а также явно или неявно присутствуют цели.

•  Направления и характеристики, по которым нужно исследовать задачу для моделирования (тип ресурса и балансов, характер операций, шкалы и др.).

•  Как использовать типовые решения из одной предметной области для, казалось бы, совсем другой области.

кратко

Емкость: «Число яблок у Оли».

Установка: «Съела». Операции установки: 1ый раз, 2ой раз.

Интервалы времени: шаги процесса, 1 раз, 2 раз.

Потоки: из емкости в установку «Съела», из нее – неизвестно куда.

Ответ. Число яблок у Оли монотонно убывает, все меньше и меньше, уменьшается по шагам: до начала процесса было 10; потом 10 – 3 = 7 и 7 – 2 = 5.

1) х1 = 10; 2) х2 = х1 – 3 = 10 – 3 = 7; 3) х3 = х2 – 2 = 7 – 2 = 5;

кратко

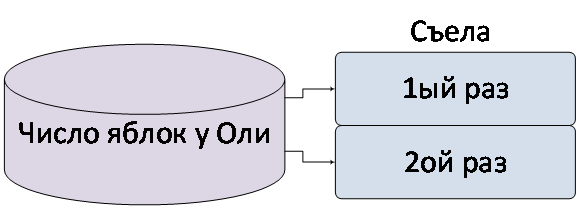
Рисунок. Схема объекта со стрелками

кратко

Лист установок, иерархия – 1 стадия, 1 установка, 2 операции, в каждой – по одному входному потоку.

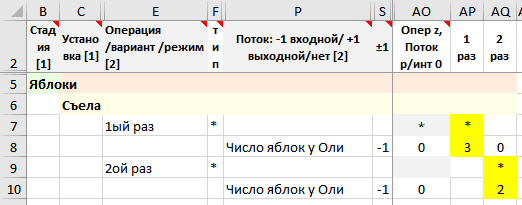
Рисунок. Фрагмент формы – стадия, установка, операция, поток

Примечания.

•  Заданы «фрагменты решения» – съедает 1й и 2й раз, и потоки – число съеденных яблок.

•  Матрица переналадок пустая, оптимизация не требуется.

Лист емкостей – 1 стадия (2я стадия пустая, «замыкающая»), 1 емкость

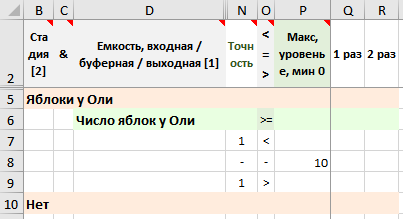
Рисунок. Фрагмент формы – стадии емкостей, емкость

Примечания.

•  Задано начальное значение яблок у Оли, т.е. считаем, что 10 яблок есть до начала процесса.

•  Ограничения на уровень в емкости отсутствуют.

•  Точность +/–1 яблоко.

На листе опций – Горизонт планирования

Рисунок. Фрагмент листа опций – горизонт планирования

Критерий не играет роли, поскольку это режим симуляции.

кратко

Листы установок и емкостей

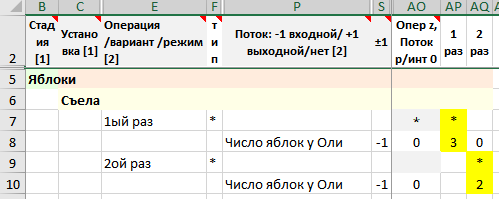
Рисунок. Расписание выполнения операций на установках

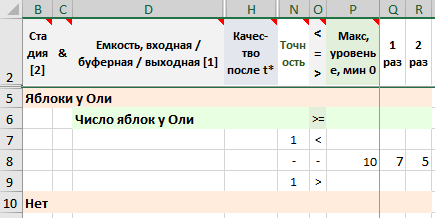
Рисунок. Расписание запасов в емкостях

Начальное значение числа яблок у Оли задано, т.е. считаем, что 10 яблок есть до начала процесса. Поэтому число яблок у Оли монотонно убывает, уменьшается по шагам: до начала процесса было 10; потом 10 – 3 = 7 и 7 – 2 = 5.

Диаграмма Ганта

Рисунок. Фрагмент расписания выполнения операций

Уровень в емкости и графики расписания потоков

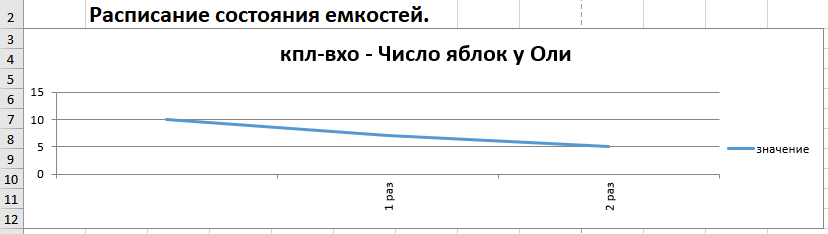
Рисунок. Графики изменения состояния емкостей

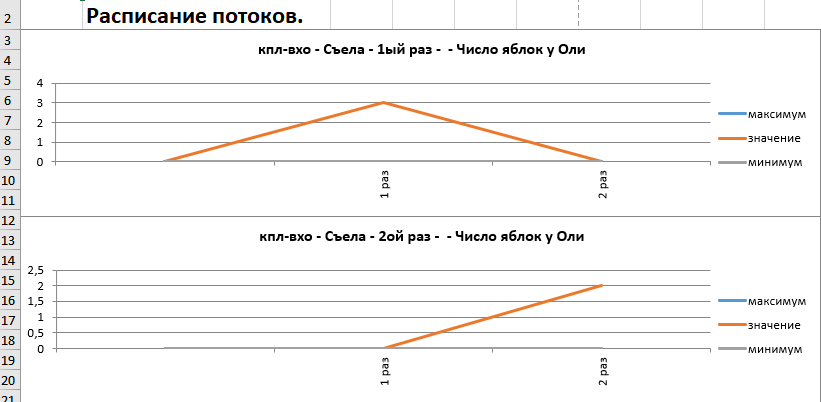
Рисунок. Графики расписания потоков

Гистограммы

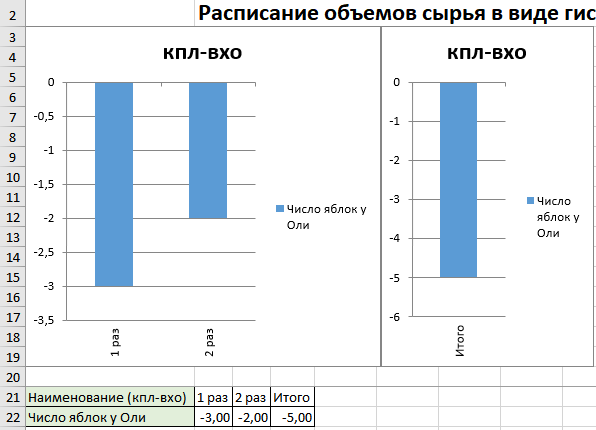
Рисунок. Гистограмма объемов потребления сырья

Отчеты

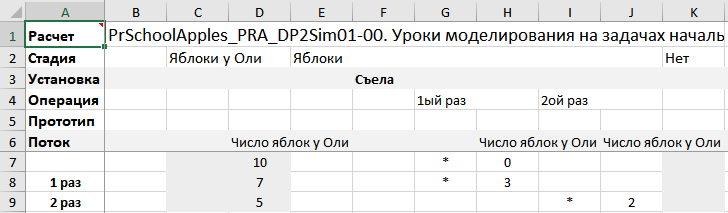
Рисунок. Отчет по установкам

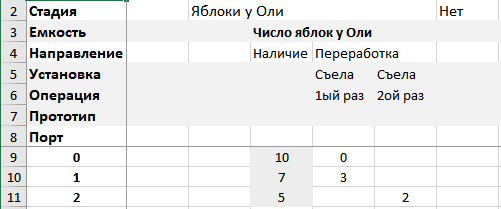
Рисунок. Отчет по емкостям

Объяснения решения

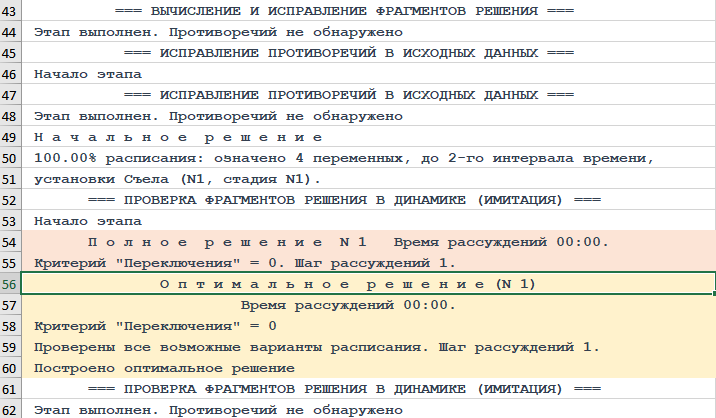
Рисунок. Фрагмент трассы объяснений хода рассуждений Решателя DP

кратко