Из одной базовой задачи строятся серии задач по возрастанию сложности. В этой серии задач отрабатываются начальные навыки оптимизации, сначала объекта в статике (1 шаг), потом – процесса, того же объекта в динамике (несколько шагов).
Особенности Объекта

подробнее…
«Сок». Дано: Оля хочет сок из яблок, но нужно их собрать, вымыть, почистить, нарезать и выжать через соковыжималку. Оля и ее друзья могут выполнить любую из этих работ, но с разным усердием и за разное время.
Определить: Кому из ребят какую работу лучше поручить? В каком порядке они должны выполнять эти работы?
Общая задача о назначениях в статике
Задача о назначении исполнителей на работы – одна из фундаментальных задач комбинаторной оптимизации или исследования операций. Задача состоит в поиске минимальной суммы весов дуг во взвешенном двудольном графе.
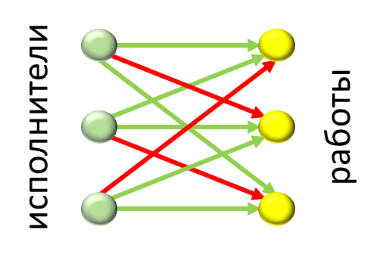
В наиболее общей форме задача формулируется следующим образом:
• Имеется множество работ и множество исполнителей. Любой исполнитель может быть назначен на выполнение любой (только одной) работы, но с неодинаковыми затратами.
• Нужно распределить работы так, чтобы выполнить их с минимальными затратами.
Если число работ и исполнителей совпадает, задача называется линейной задачей о назначениях. Обычно, если говорят о задаче о назначениях без дополнительных условий, имеют в виду линейную задачу о назначениях.
Задачу о назначениях можно считать частным случаем транспортной задачи, для которой мощности поставщиков и потребности клиентов равны 1 (и обычно совпадает размерность).
Практические примеры
• Назначение такси на маршрут с минимальным временем ожидания клиента.
• Распределение ремонтных бригад по участкам работ.
• Формирование локомотивных бригад в зависимости от класса квалификации и стажа работы машинистов.
Особенности базовой модели
Дано: Исполнители, которых можно назначать только на одну работу.
Работы, для выполнения которых можно назначать только одного исполнителя.
Определить: назначение исполнителей на работы по критерию минимума затрат на выполнение работ.
Примечания.
• Для повышения эффективности уместно распределять меньшее число объектов на большее, т.е. если число работ больше числа исполнителей, то распределять исполнителей, иначе работы по исполнителям. Базовая модель строится «от исполнителей», т.к. число исполнителей меньше числа работ.
• Множество установок соответствует множеству исполнителей. Операции установки отражают назначение исполнителя на выполнение определенной работы.
• Потоками операции являются часть работы, которая может выполняться данным исполнителем. Величина потока, равная 1 означает, что исполнитель выполняет всю работу.
• Для потоков операций установок задается ограничение баланса.
• Для задания минимального и максимального объема работ используются ограничения на границы емкости в конце горизонта.
• Для задания возможностей исполнителя по выполнению работ используются остатки емкостей и границы емкостей в конце горизонта.
• Критерий – минимум суммарных затрат на выполнение работ. Для минимизации затрат используется критерий прибыли/издержек от выполнения операций. Стоимость выполнения операции равна затратам от назначения исполнителя на работу, деленным на 2, поскольку объем работы в операции учитывается дважды – один входящий поток от исполнителя, другой выходящий поток к работе.
кратко
